Implementing Bicubic Scaling in TGSI

This post has been pending for some time now. I have been working on VDPAU state tracker for the past 2 months and have implemented luma keying and bicubic scaling and currently working on lanczos scaling. I will be writing about image scaling algorithms and my implementation of bicubic shader in this post.

Image Scaling

We are given a image at a particular resolution say 300x300 in the form of a 2D matrix which contains the RGB values. Let’s say we need to scale the image to 3x. So the final output will be a 900x900 matrix. Out of the 900x900 = 810000 values we know 90000(300x300) values but we need to find the remaining values by extrapolating the given values.

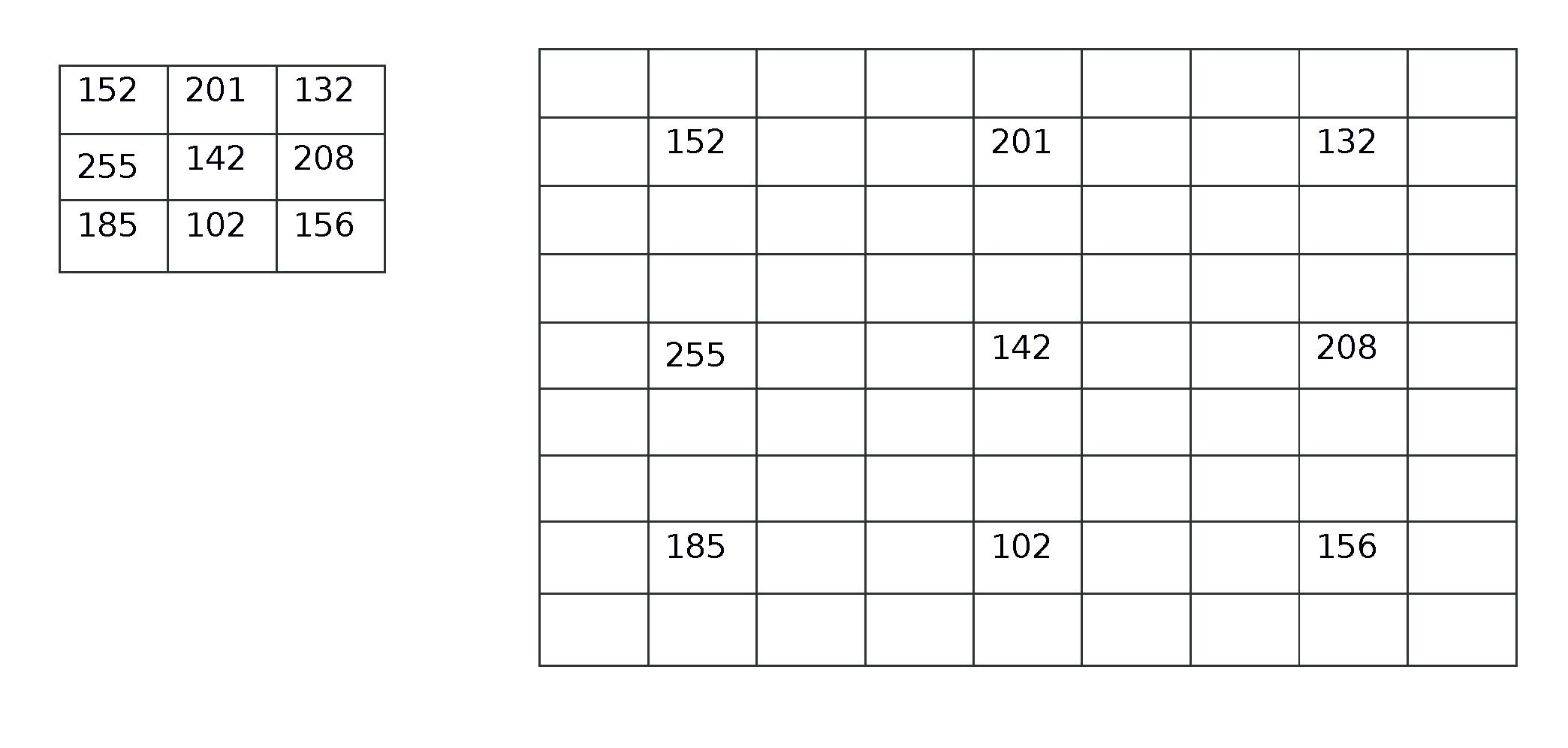
The fuction that you use to extrapolate the image determines the type of filter. All the functions us the values of the pixels present in the original image to expolate the pixels. The most basic scaling is the Nearest-neighbor interpolation, as the name suggests the value of the pixel is same as the value of the nearest pixel (which was part of the original image). The other important and widely used method is bilinear interpolation which uses linear interpolation to calculate the pixel values.

Bicubic Interpolation

As is obivous we are going to use a bicubic fuction for interpolation in the bicubic filter. The specific function that we are going to focus on is cubic Hermite spline (given in the figure below with a = -2).

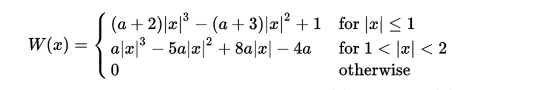
In a bicubic interpolater we use 16 neighbouring pixels to calculate the pixel value. The value of the pixel not only depends on its neighbouring pixels but also depends on the distance of the neighbouring pixels from the pixel. Bicubic interpolation involves cubic interpolation along x axis applying it on 4 pixel at a time and then applying a cubic interpolation to the resultant of the previous 4 cubic interpolation along the y axis. Confusing right? It will get clear once once we look at the formulas.

1-D Cubic Interpolation

For one dimensional cubic interpolation we require 4 points. So given value of pixel at x=-1,0,1 and 2, I can calculate the value of pixel at any position between 0 and 1 by following function p(t):

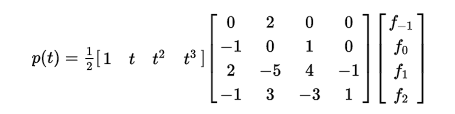
Where t is the x-coordinate of the point.

2-D Bicubic interpolation

For the bicubic interpolation we need to apply cubic interpolation 5 times, 4 along x-axis and one along y-axis.

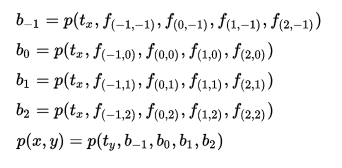
Enough with the theory let’s look at the code. First we will look at the code for the cubic interpolator i.e. code to calculate p(t). We will divide calculation of p(t) in two parts first we will multiply the pixel values of the four points with the 4x4 matrix and store the result in 4 temp registers.

   /*
    * |temp[0]|   |  0  2  0  0 |  |tex_a|
    * |temp[1]| = | -1  0  1  0 |* |tex_b|
    * |temp[2]|   |  2 -5  4 -1 |  |tex_c|
    * |temp[3]|   | -1  3 -3  1 |  |tex_d|
    */
   ureg_MUL(shader, temp[0], tex_b, ureg_imm1f(shader, 2.0f));

   ureg_MUL(shader, temp[1], tex_a, ureg_imm1f(shader, -1.0f));
   ureg_MAD(shader, temp[1], tex_c, ureg_imm1f(shader, 1.0f),
            ureg_src(temp[1]));

   ureg_MUL(shader, temp[2], tex_a, ureg_imm1f(shader, 2.0f));
   ureg_MAD(shader, temp[2], tex_b, ureg_imm1f(shader, -5.0f),
            ureg_src(temp[2]));
   ureg_MAD(shader, temp[2], tex_c, ureg_imm1f(shader, 4.0f),
            ureg_src(temp[2]));
   ureg_MAD(shader, temp[2], tex_d, ureg_imm1f(shader, -1.0f),
             ureg_src(temp[2]));

   ureg_MUL(shader, temp[3], tex_a, ureg_imm1f(shader, -1.0f));
   ureg_MAD(shader, temp[3], tex_b, ureg_imm1f(shader, 3.0f),
            ureg_src(temp[3]));
   ureg_MAD(shader, temp[3], tex_c, ureg_imm1f(shader, -3.0f),
            ureg_src(temp[3]));
   ureg_MAD(shader, temp[3], tex_d, ureg_imm1f(shader, 1.0f),
            ureg_src(temp[3]));

Easy enough right.

Now let’s look at the code to multiply temp registes with t, which is provided to us as a argument, we will see how to calculate ‘t’ it in the bicubic code. This code is mostly trivial.

   /*
    * t_2 = t*t
    * o_fragment = 0.5*|1  t  t^2  t^3|*|temp[0]|
    *                                   |temp[1]|
    *                                   |temp[2]|
    *                                   |temp[3]|
    */

   ureg_MUL(shader, t_2, t, t);
   ureg_MUL(shader, temp[4], ureg_src(t_2), t);

   ureg_MUL(shader, temp[4], ureg_src(temp[4]), ureg_src(temp[3]));
   ureg_MUL(shader, temp[5], ureg_src(t_2), ureg_src(temp[2]));
   ureg_MUL(shader, temp[6], t, ureg_src(temp[1]));
   ureg_MUL(shader, temp[7], ureg_imm1f(shader, 1.0f), ureg_src(temp[0]));
   ureg_ADD(shader, temp[8], ureg_src(temp[4]), ureg_src(temp[5]));
   ureg_ADD(shader, temp[9], ureg_src(temp[6]), ureg_src(temp[7]));

   ureg_ADD(shader, temp[10], ureg_src(temp[8]), ureg_src(temp[9]));
   ureg_MUL(shader, o_fragment, ureg_src(temp[10]), ureg_imm1f(shader, 0.5f));

The one intriguing thing about the code is the number of temp registers I use to calculate the value this could be easily avoided, that’s what I thought but when I tried reducing there were errors and artifacts in the output. Even now I don’t know the exact reason for the artifacts but using many temp registers cleared the errors.

Now we need to write the code for the bicubic interpolation which calls the above function 5 times. The toughest part of the entire code is to calculate t while calling the cubic interpolator

   half_pixel = ureg_DECL_constant(shader, 0);
   o_fragment = ureg_DECL_output(shader, TGSI_SEMANTIC_COLOR, 0);

   /*
    * temp = (i_vtex - (0.5/dst_size)) * i_size)
    * t = frac(temp)
    * vtex = floor(i_vtex)/i_size
    */
   ureg_SUB(shader, ureg_writemask(t_array[21], TGSI_WRITEMASK_XY),
            i_vtex, half_pixel);
   ureg_MUL(shader, ureg_writemask(t_array[22], TGSI_WRITEMASK_XY),
            ureg_src(t_array[21]), ureg_imm2f(shader, video_width, video_height));
   ureg_FRC(shader, ureg_writemask(t, TGSI_WRITEMASK_XY),
            ureg_src(t_array[22]));

   ureg_FLR(shader, ureg_writemask(t_array[22], TGSI_WRITEMASK_XY),
            ureg_src(t_array[22]));
   ureg_DIV(shader, ureg_writemask(t_array[22], TGSI_WRITEMASK_XY),
            ureg_src(t_array[22]), ureg_imm2f(shader, video_width, video_height));
   ureg_ADD(shader, ureg_writemask(t_array[22], TGSI_WRITEMASK_XY),
            ureg_src(t_array[22]), half_pixel);

First we subtract the offset of 0.5 pixel from the coordinate because the pixel center is at 0.5. Now the t_array[21] holds the coordinates divided by the dst width/height. We multiply it with src (width, height) and taking fraction of this value we get the value of t which needed to be in the frame of src coordinates, that explains the reason for multiplying it with src width/height. By applying the FLR on the value in t_array[22] gives us the point which had a pixel value from the original src and not the interpolated one. Now we need 15 more points from the original image for the interpolation. This could be achieved by adding offsets to the original points that we have got so we convert the point to dst coordinates. Finally t_array[22] conatins the refernce point from which the other 15 points will be obatined, we have also added the 0.5 offset to get the value in dst coordinates.

The next part involves adding offsets to the points and storing the texture of this points in the temp array. Now we call our cubic interpolater function 5 times with the respective values.

   /*
    * t_array[0..*] = vtex + offset[0..*]
    * t_array[0..*] = tex(t_array[0..*], sampler)
    * t_array[16+i] = cubic_interpolate(t_array[4*i..4*i+3], t_x)
    * o_fragment = cubic_interpolate(t_array[16..19], t_y)
    */
   vtex = ureg_src(t_array[22]);
   for (i = 0; i < 16; ++i) {
        ureg_ADD(shader, ureg_writemask(t_array[i], TGSI_WRITEMASK_XY),
                  vtex, ureg_imm2f(shader, offsets[i].x, offsets[i].y));
        ureg_MOV(shader, ureg_writemask(t_array[i], TGSI_WRITEMASK_ZW),
                  ureg_imm1f(shader, 0.0f));
   }

   for (i = 0; i < 16; ++i) {
      ureg_TEX(shader, t_array[i], TGSI_TEXTURE_2D, ureg_src(t_array[i]), sampler);
   }

   for(i = 0; i < 4; ++i)
      create_frag_shader_cubic_interpolater(shader, ureg_src(t_array[4*i]),
              ureg_src(t_array[4*i+1]), ureg_src(t_array[4*i+2]),
              ureg_src(t_array[4*i+3]), ureg_scalar(ureg_src(t),
              TGSI_SWIZZLE_X), t_array[16+i]);

   create_frag_shader_cubic_interpolater(shader, ureg_src(t_array[16]),
            ureg_src(t_array[17]), ureg_src(t_array[18]),
            ureg_src(t_array[19]), ureg_scalar(ureg_src(t),
            TGSI_SWIZZLE_Y), o_fragment);

This completes the post then. I have tried to explain the bicubic interpolation and its implementation in detail but whom am I kidding, I am not that good in explaining, if there is something wrong or something that you haven’t understood please feel free to comment.